[BFS] 백준 7562. 나이트의 이동 (feat. 2차원 배열이동)

 

 

문제

체스판 위에 한 나이트가 놓여져 있다. 나이트가 한 번에 이동할 수 있는 칸은 아래 그림에 나와있다. 나이트가 이동하려고 하는 칸이 주어진다. 나이트는 몇 번 움직이면 이 칸으로 이동할 수 있을까?

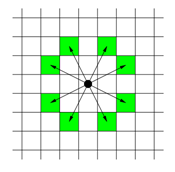
입력

입력의 첫째 줄에는 테스트 케이스의 개수가 주어진다.

각 테스트 케이스는 세 줄로 이루어져 있다. 첫째 줄에는 체스판의 한 변의 길이 l(4 ≤ l ≤ 300)이 주어진다. 체스판의 크기는 l × l이다. 체스판의 각 칸은 두 수의 쌍 {0, ..., l-1} × {0, ..., l-1}로 나타낼 수 있다. 둘째 줄과 셋째 줄에는 나이트가 현재 있는 칸, 나이트가 이동하려고 하는 칸이 주어진다.

출력

각 테스트 케이스마다 나이트가 최소 몇 번만에 이동할 수 있는지 출력한다.

---

문제 요약

체스판 나이트 이동, 목적지까지 얼마나 걸려?

DFS와 BFS의 차이점

1. 문제에서 최단 경로 언급 => BFS

2. BFS가 실행시간이 다소 빠른 경향

 

코드 프레임에서의 차이점

# BFS는 함수 선언 내부에 재귀로 호출하는 대신

# q를 append 하고 소진(popleft)할 때까지 반복문으로 진행
# 결국 전체코드에서 BFS 호출은 한번만 하게 됨

# BFS수행하고 나서 그래프의 목적지(마지막값) 좌표를 출력하거나, 함수 내부에서 출력하며 종료

import sys
from collections import deque
sys.stdin = open('./BFS/input.txt','rt')

t = int(input())

dx = [-2, -1, 1, 2, -2, -1, 1, 2]
dy = [ 1, 2, 2, 1,  -1, -2, -2, -1]

# BFS는 재귀가 필요없구나...
# 함수 안에 재귀 대신 q 반복문으로 푸는구나...
# BFS 호출은 한번만 하면 되는 것..!

def BFS(x,y, ox, oy):
    global l
    q = deque()
    q.append([x,y])
    while q:
        a,b = q.popleft()
        if a==ox and b==oy:
            return
        for k in range(8):
            nx = a+dx[k]
            ny = b+dy[k]
            if 0<=nx<l and 0<=ny<l and check[nx][ny] == False:
                check[nx][ny] = True
                q.append([nx, ny])
                g[nx][ny] = g[a][b] + 1

for i in range(t):
    l = int(input())
    g = [[0]*(l) for _ in range(l)]
    check = [[False]*(l) for _ in range(l)]
    x, y = map(int, input().split())
    mx, my = map(int, input().split())
    
    BFS(x, y, mx, my)
    print(g[mx][my]) # 최종값 출력